不等辺三角形 三角形(さんかくけい、さんかっけい、拉 triangulum, 独 Dreieck, 英, 仏 triangle, (古風) trigon) は、同一直線上にない3点と、それらを結ぶ3つの線分からなる多角形。その3点を三角形の頂点、3つの線分を三角形の辺という。 点A, 点B, 点不等辺三角形の選択した3つの入力値から他の要素の値を計算します。 入力指定 3辺abc 2辺abと高さ (Cは鋭角) 2辺abと高さ (Cは鈍角) 2辺bcと高さ (BとCが鋭角) 2辺bcと高さ (BかCが鈍角) 2辺abと夾角C 辺aと高さと角C 2角BCと夾辺a 2角BCと高さ 面積と2辺ab (Cは鋭角) 面積と2辺ab (Cは鈍角) 面積と2角BC 面積と辺解答: Myersの三角形 • 有効な不等辺三角形 • 有効な正三角形 • 有効な二等辺三角形 • 有効な二等辺三角形で 3種類の辺の組み合わせ • 長さが0の辺 • 長さが負の値の辺 • 2辺の和がもう1辺と等しい • 2辺の和がもう1辺と等しい

二等辺三角形の底角は本当に等しいのか ひと筋縄ではいかない証明 ブルーバックス編集部 ブルーバックス 講談社 1 4
不等辺三角形 定義
不等辺三角形 定義-不等辺三角形は、すべての辺と角度が等しくない、つまり互いに異なることを特徴とする三角形です。 それはあなたに興味があるかもしれません: 不等辺三角形。 ジオメトリ。 角度に応じた三角形の種類 三角形は、直線(90°に等しい)の角度の幅に従って分類できます。三角形という図形の性質・定義を規定するものは何か。 〇 永続的理解 三角形は,図形の構成要素に着目することで,二等辺三角形,正三角形,不等辺三角形に分類・整理する ことができる。 単元の目標




マイヤーズの三角形問題 テストの基礎 Qbookアカデミー
13/6/21 補足:ピタゴラス数(整数の話題) 一般に,三つの自然数の組 ( a, b, c) (a,b,c) (a,b,c) が三平方の定理の式 a 2 b 2 = c 2 a^2b^2=c^2 a2 b2 = c2 を満たすとき, ( a, b, c) (a,b,c) (a,b,c) を ピタゴラス数 と呼びます。 有名なピタゴラス数として,となる.これで三角形の成立条件の不等式が示された. 十分条件を示す. を満たす3正数 がある. を3辺とする三角形が存在することは, 次のように図形的に示される. つまり,長さ の線分 をとる. 点 を中心に半径 の円と, 点 を中心に半径 の円をかく.三角形に対して,一般的に各頂点の向かいの辺の長さを,頂点を表す文字の小文字を使って表します。 この場合, h = AB , a = BH , b = AH となります。 このとき, ∠A に対して 辺 AB を 斜辺 辺 AH を 底辺 (または 隣辺 ) 辺 BH を 対辺 といいます。 そして, ∠A の大きさによってそれぞれの辺の比の値が決まります。 3つの辺の比 a h , b h , a b にはそれぞれ
直角三角形の辺の長さの求め方と計算ツール 具体例で学ぶ数学 不等辺三角形 高精度計算サイト;Ama04 練習問題へ abdu は直角二等辺三角形,u bcd は30 °,60 °の角をもつ直角三角形であるから,3 辺 のうちの1 辺の長さがわかると残りの辺の長さも求められる。 ここでは,共通のbd の長さを 調べると,xの値が求められる。 abhu とu ach に分けて,それぞれがどのような辺の比をもつ三角形(さんかくけい、さんかっけい、拉 triangulum, 独 Dreieck, 英, 仏 triangle, (古風) trigon) は、同一直線上にない3点と、それらを結ぶ3つの線分からなる多角形。 その3点を三角形の頂点、3つの線分を三角形の辺という。 目次 1 記法・定義 11 三角形を成り立たせる3辺 (三角形の成立条件)
定義の補足(命題1ー28)(外角・内対角(平行線)) による。 ゆえに 底辺EBは 底辺FCに等しく、 三角形EABは 三角形FDCに等しいであろう。 命題1ー4(2辺挟角相等) による。 となっている。 双方から DHEが引き去られたとせよ。実践記録算数4年 1.はじめに 現在,学習指導要領のねらいである「生きる力」の育成,とりわけその知の要素である「確かな学力」の育成が求められている。 そのためには,個々の子どもの実態に応じたきめ細かな指導を行う必要がある。 「発展的な三平方の定理直角三角形の辺の長さを計算する4つの問題の 答1448 直角三角形の2辺 ★ ヤドカリの 気ままな数学 ★;




直角二等辺三角形 Wikipedia




直角二等辺三角形 Wikiwand
数学における三角不等式(さんかくふとうしき、英 triangle inequality )は、任意の三角形に対してその任意の二辺の和が残りの一辺よりも大きくなければならないことを述べるものである 。 三角形の三辺が x, y, z で最大辺が z とすれば、三角不等式は mathz \leq x y/mathということで, \(C = 60°\) の三角形です 正弦定理は比例式 次の (3) は,辺の長さと角の \(\sin\) が混在しています \a\sin A b\sin B = c\sin C\ ただし,私的には,この式を見た瞬間にどんな三角形をかを答えてほしいと考えます 不等辺三角形のときは 3 を返す testScalene 二等辺三角形と同様に tests をクリックしてテンプレートを呼び出し、testScalene を定義(コピペ and/or 写経 → Ctrl S でコンパイル → Ctrl Shift F でフォーマット → Ctrl S で再コンパイル)後、Ctrl J → M でテストを走らせ、失敗(イエローバー)を
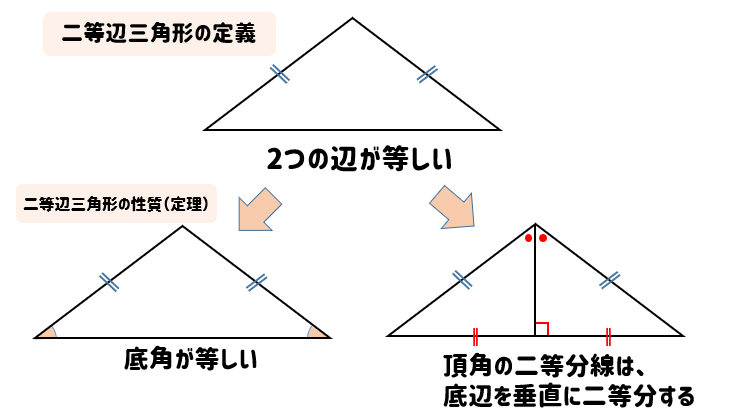



二等辺三角形の定義と性質をサクッと確認しておこう 数スタ
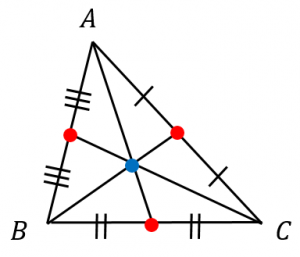



三角形の重心の定義といろいろな求め方 具体例で学ぶ数学
三辺形のうち、 等辺三角形とは三つの等しい辺をもつもの、 二等辺三角形とは二つだけ等しい辺をもつもの、 不等辺三角形とは三つの不等な辺をもつものである。 等辺とはすべての辺が等しいこと。 (以下、定義1ーの補足(等辺) という。) 三角形で様々な三角形を作る。辺の長さの違い による分類方法を考える。 ②2つの分類方法で,それぞれ3つの集 合を作る。 ③2辺の長さが等しい三角形を紙に写し 取り,辺の長さなどを調べて,二等辺 三角形の定義を知る。 ④2辺の長さが等しい三角形を紙に写し三角形の3辺の長さから面積を求めましょう お題の三角形については \a = 7,\quad b = 5,\quad c = 8\ が,分かっているということです どの角の大きさも分っていません んっ! 待ってください・・・この三角形は,どこかで見たことがあるような気がします




不等辺三角形の証明 電子単話 感想 Bl情報サイト ちるちる




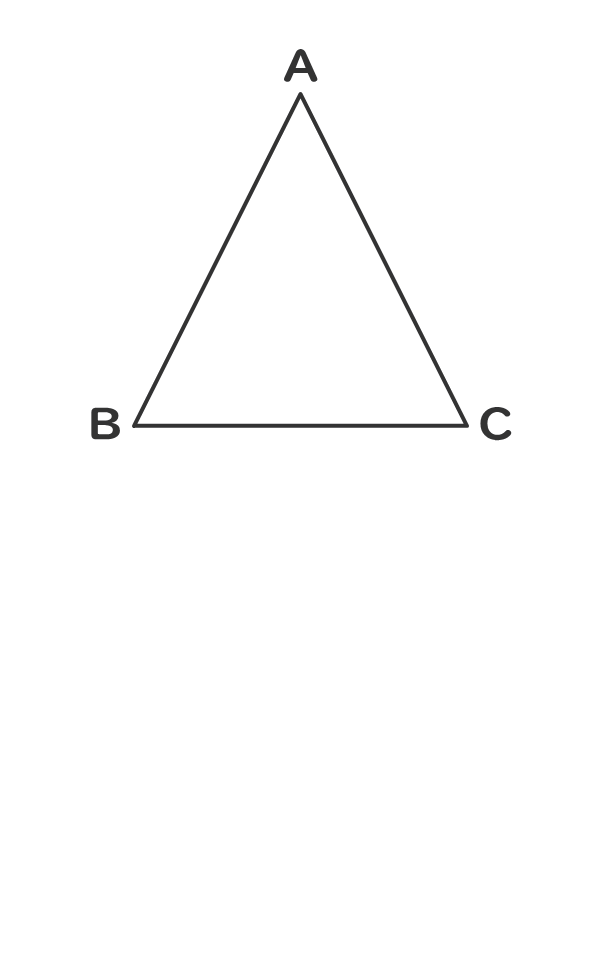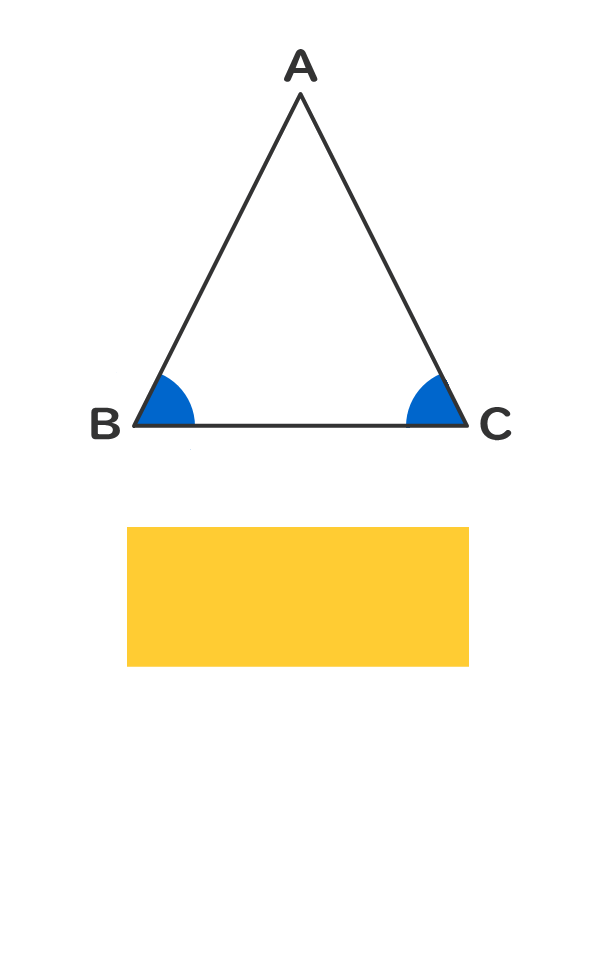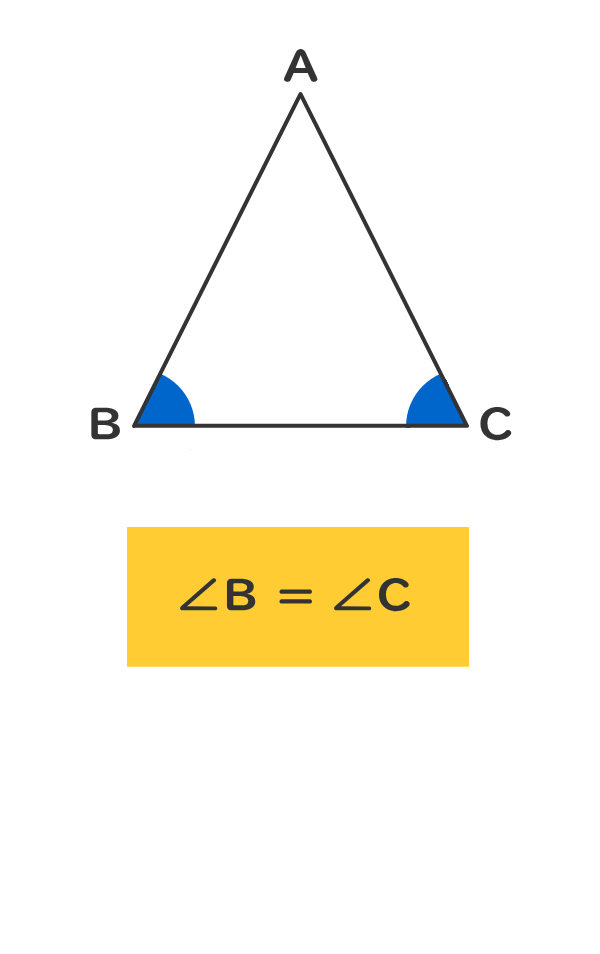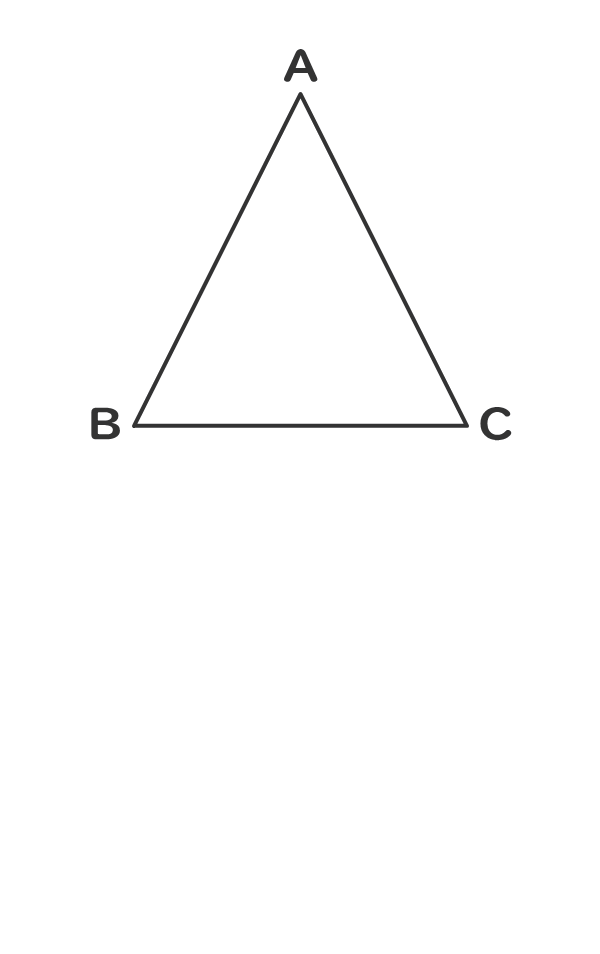
二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者
6/3/21 三角形の成立条件に登場する不等式を三角不等式といいます。 三角不等式は様々な「長さ」に拡張されています。 →いろいろな三角不等式(絶対値,複素数,ベクトル) 三本の不等式を a a a について解くことで,条件を ∣ b − c ∣ < a < b c bc三辺形において、三辺が等しいものを正三角形 せいさんかくけい, ἰσόπλευρος τρίγωνος, equilateral triangle 、二辺が等しいものを二等辺三角形 にとうへんさんかくけい, ἰσοσκελής τρίγωνος, isosceles triangle 、すべて異なるものを不等辺三角形 ふとうへんさんかくけい, σκαληνός凸多角形の定義と認識方法 点列P=(p 0, p 1, p 2, , p n=p 0)が凸多角形を成すかどうかの判定: s ij 頂点p iとpjを結ぶ線分(対角線),ij≧2 仮定:多角形の辺は反時計回り(内部は辺の左)に順序付




三角形の種類を判定しよう 電験3種web



斜辺の長さが10 の直角二等辺三角形の面積の求め方を教えてください 直角 二 等辺 三角形 斜辺
三角形(さんかくけい、さんかっけい、拉 triangulum, 独 Dreieck, 英, 仏 triangle, (古風) trigon) は、同一直線上にない3点と、それらを結ぶ3つの線分からなる多角形。 その3点を三角形の頂点、3つの線分を三角形の辺という。 記法・定義 点A, 点B, 点C を頂点とする三角形は記号 を用いて ABC と表 じすがなぼ まずは歌いましょう。wwwyoutubecom参考記事 三角形の五心の覚えておくべき性質を整理 高校数学の美しい物語 重心 三角形に対して、辺の中点をとする。辺, 辺についても同様に考えてを定義する。定理 直線は一点で交わる。この一点を重心という。3辺の値のうち、2辺が等しい場合は、画面に「2等辺三角形」と出力する。 24 不等辺三角形 3辺の値が全て異なる場合、画面に「不等辺三角形」と 不等辺三角形の証明 あがた愛の電子書籍・漫画(コミック)を無料で試し読み巻。



1



1
不等辺三角形とは コトバンク デジタル大辞泉 不等辺三角形の用語解説 どの辺の長さも等しくない三角形。 直角二等辺三角形に関連する問題って、定義や性質・証明を知らないとなかなか解きづらくなりますよね。デジタル大辞泉 「不等辺三角形」の解説 ふとうへん‐さんかくけい不等辺三角形 どの辺の長さも等しくない三角形。特に,\(30°\) や \(45°\) などの角のとき,直角三角形の辺の比を使った定義と比較してください もちろん,同じ意味なので・・・そのことを確認しましょう 三角方程式 三角比の意味が確認できたので,本日のお題,三角方程式・不等式を解いていきましょう




基本のtriangles 三角形 に関する英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強




二等辺三角形の定義と性質 問題の解き方 数学fun
7/5/21 また、三角形の 3 つの辺の長さに注目して、 3 つの辺の長さがすべて異なる三角形を不等辺三角形(図 2)という。 2 つの辺の長さが等しい三角形を二等辺三角形(図 5)という。6/3/21 三角形の五心の覚えておくべき性質を整理 レベル ★ 最難関大受験対策 平面図形 更新日時 三角形の五心の定義と重要な性質をまとめました。 三角形の五心は有名で豊かな性質を持っており,数学オリンピックの初等幾何の証明問題では超頻出数学 、 三角不等式 は、 三角形 の場合、任意の2つの辺の長さの合計が残りの辺の長さ以上でなければならないと述べています。このステートメントでは、 縮退した三角形 を含めることができますが、一部の作成者、特に基本ジオメトリについて書いている作成者は、この可能性を除外し




余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ
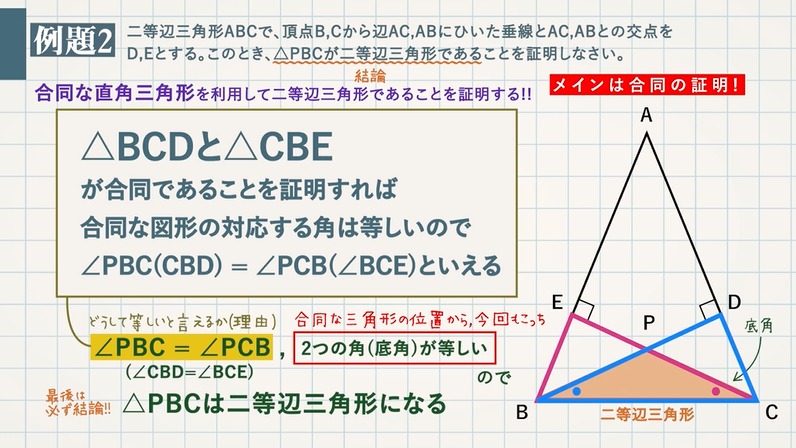



二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者




二等辺三角形と正三角形 算数用語集




三角形 Wikipedia
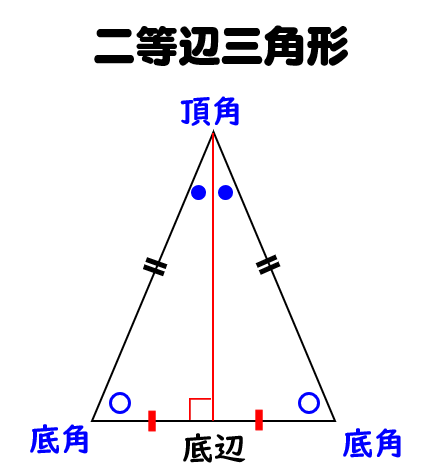



二等辺三角形の定義と性質 問題の解き方 数学fun




基本のtriangles 三角形 に関する英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強




二等辺三角形や直角三角形って英語で何て言うの 三角形の種類について 40代 50代 60代 シニア 初心者からやり直し英会話 英語学習法



二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係
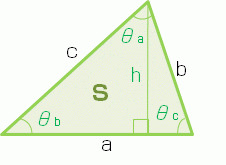



三角形の公式 Wakatta
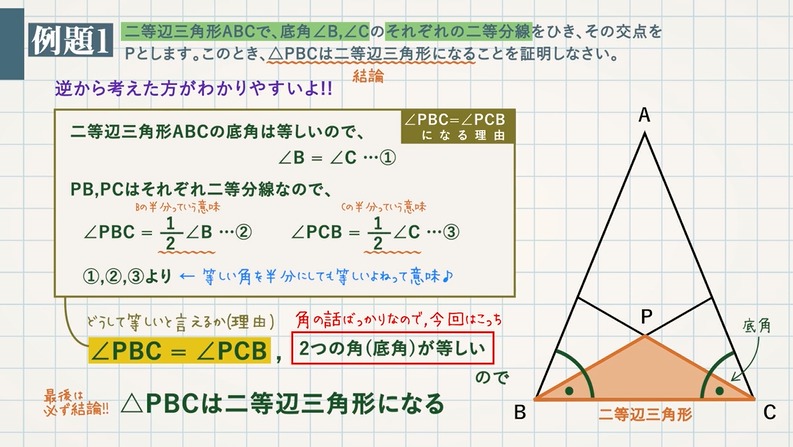



二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者




マイヤーズの三角形問題 テストの基礎 Qbookアカデミー



生花の概説



斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める
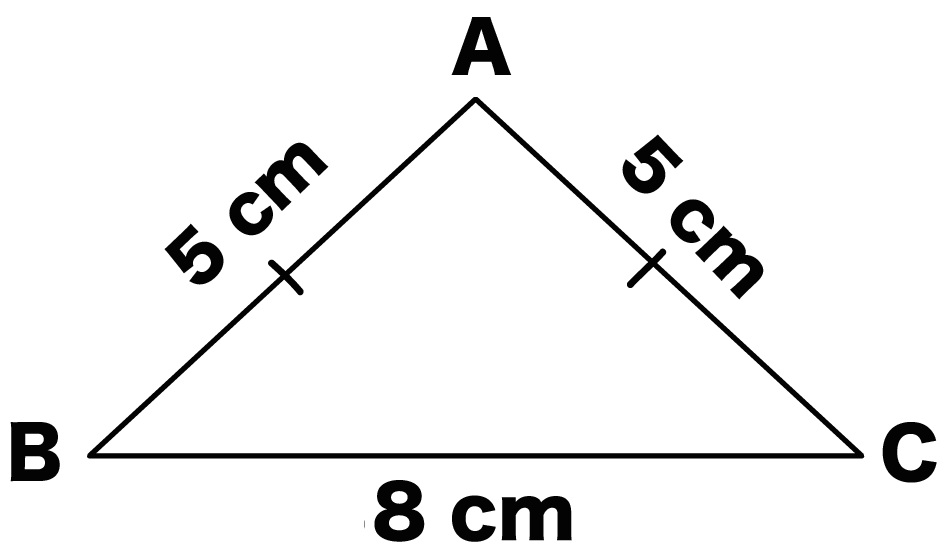



簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
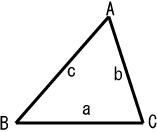



ファイル 不等辺三角形 Png Wikipedia
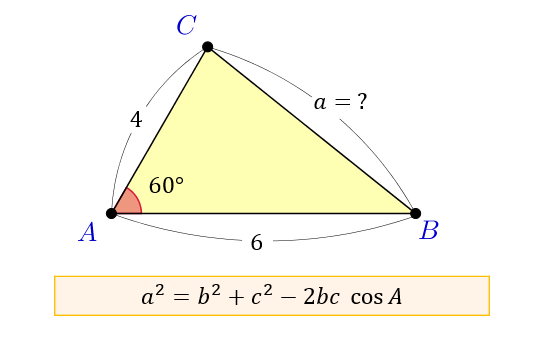



余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ




基本のtriangles 三角形 に関する英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強




頂角36度の二等辺三角形の辺の比を教えてください 頂角36度の二等辺三 数学 教えて Goo



数学 色々な三角形の英単語まとめ 二等辺三角形 直角三角形ほか 英単語project




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比



53 不等辺三角形的発想 庭語り どっとこむ エクステリアショップの未来創造集団




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学



不等辺三角形 高精度計算サイト




二等辺三角形の定義と性質をサクッと確認しておこう 数スタ




二等辺三角形の定義と性質 問題の解き方 数学fun



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン
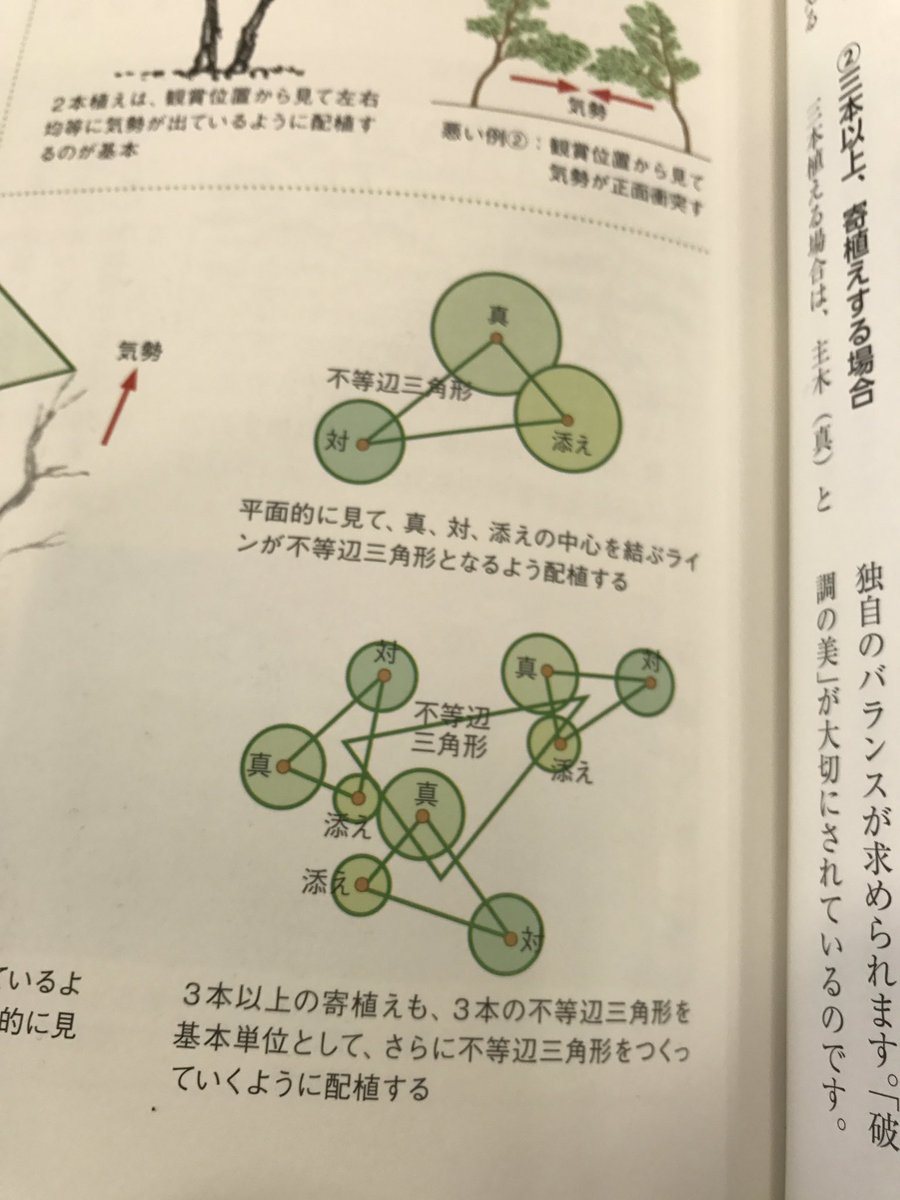



不等辺三角形のフラクタル 宇田川辰彦監修 庭師が教える 図解 日本庭園の見方 楽しみ方 勉強メモ Togetter




黄金三角形による18 シリーズの三角比 おいしい数学




不等辺三角形 至急ご回答お待ちしております 不等辺三角形について その他 学校 勉強 教えて Goo




3 おかしな不等辺三角形 Imujii S Page
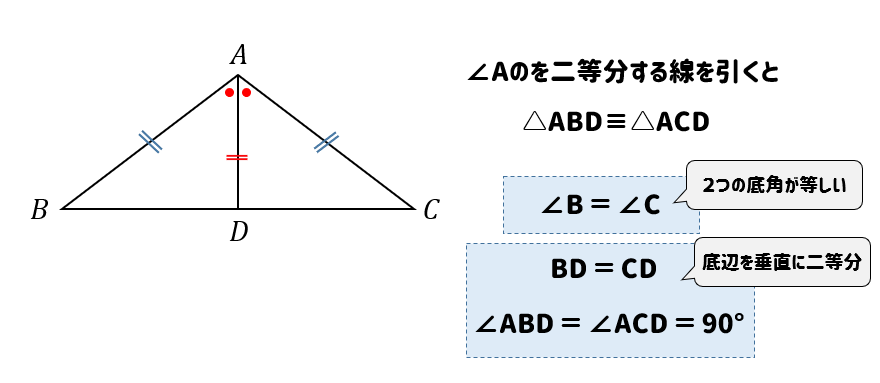



二等辺三角形の定義と性質をサクッと確認しておこう 数スタ




リーマン予想証明後の数学30 直角二等辺三角形のギャスケット 発想力教育研究所 素数誕生のメカニズム
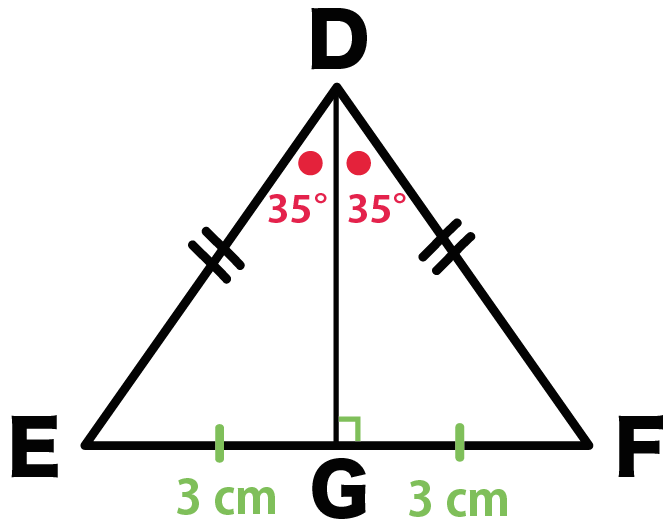



3分でわかる 二等辺三角形の2つの定理 性質 Qikeru 学びを楽しくわかりやすく
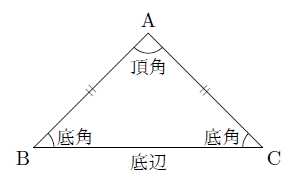



二等辺三角形の性質 まなびの学園




鋭角三角形 Wikipedia




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




小学6年生で三角形の面積求め方わかりません 小学6年生の親です 学 数学 教えて Goo



三角形の種類を判定しよう 電験3種web



1



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典




基本のtriangles 三角形 に関する英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット
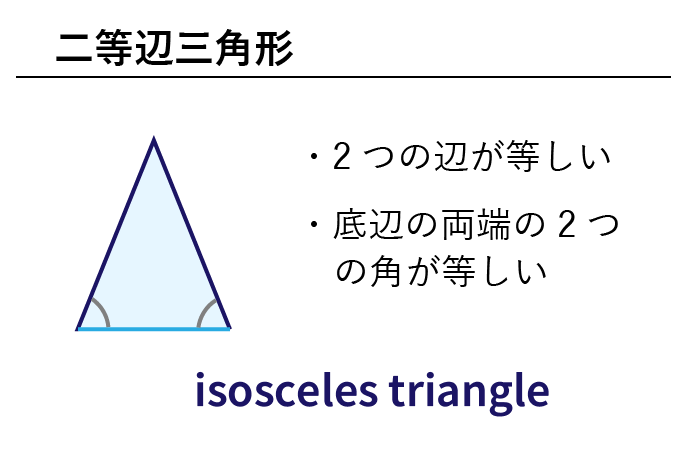



数学 色々な三角形の英単語まとめ 二等辺三角形 直角三角形ほか 英単語project




不等辺三角形の意味 用法を知る Astamuse




2 2 内外を繋ぐ広縁と濡縁の活かし方 エクステリア All About




不等辺三角形 至急ご回答お待ちしております 不等辺三角形について その他 学校 勉強 教えて Goo




号 テスト設計 技法 の必要性 Kouichi Akiyama Note



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典



斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める



このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋
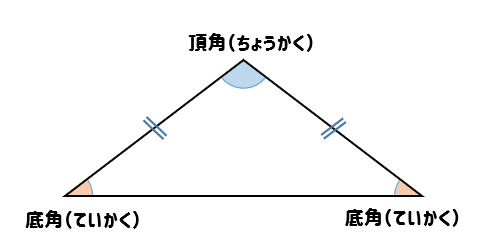



二等辺三角形の定義と性質をサクッと確認しておこう 数スタ
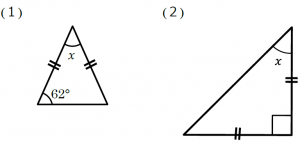



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン




基本のtriangles 三角形 に関する英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強
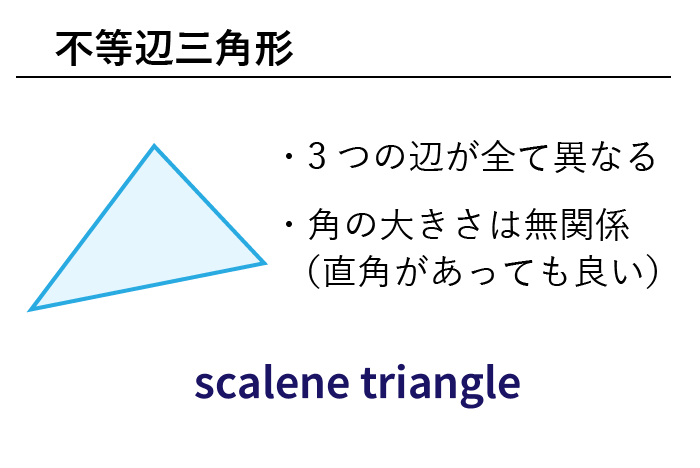



数学 色々な三角形の英単語まとめ 二等辺三角形 直角三角形ほか 英単語project




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
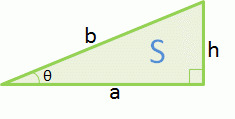



三角形の公式 Wakatta



台形と不等辺四角形 復氷




基本のtriangles 三角形 に関する英語表現をマスターしよう ゆう アメリカ生活終了 英語勉強




直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学
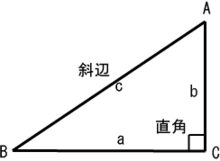



三角形 Wikipedia




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学



不等辺三角形で高さ34 1cm 底辺32 6cmの場合の斜辺の長さはどうすれ Yahoo 知恵袋




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




ビキニが似合う体型のポイント 不等辺三角形 とは Fitness Love



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン
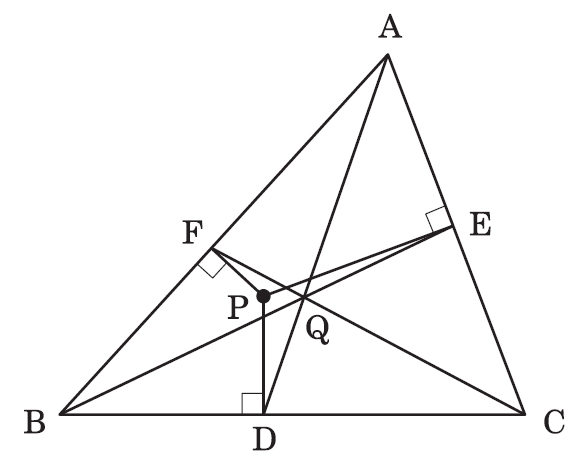



出題 年2月号掲載分 応募締切 2月8日 解答 年5月号掲載 Web日本評論



二等辺三角形




三角形 Wikipedia
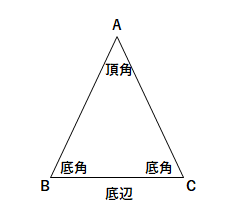



中2数学 二等辺三角形の定義と性質 Examee




二等辺三角形の底角は本当に等しいのか ひと筋縄ではいかない証明 ブルーバックス編集部 ブルーバックス 講談社 1 4




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ




二等辺三角形の定理や性質 底角が等しいことは絶対に覚えよう 中学や高校の数学の計算問題




不等辺三角形の意味 用法を知る Astamuse
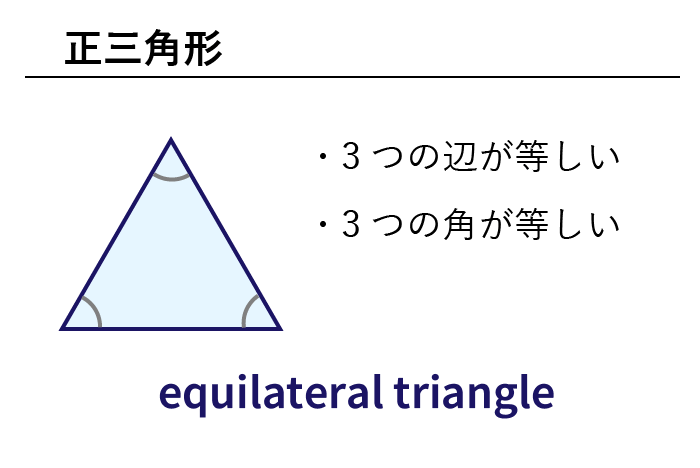



数学 色々な三角形の英単語まとめ 二等辺三角形 直角三角形ほか 英単語project




数学 中2 64 二等辺三角形 Youtube



ゆっるゆる アクアリウムと日本の庭園にみる伝統石組みレイアウト Mobi Aqua
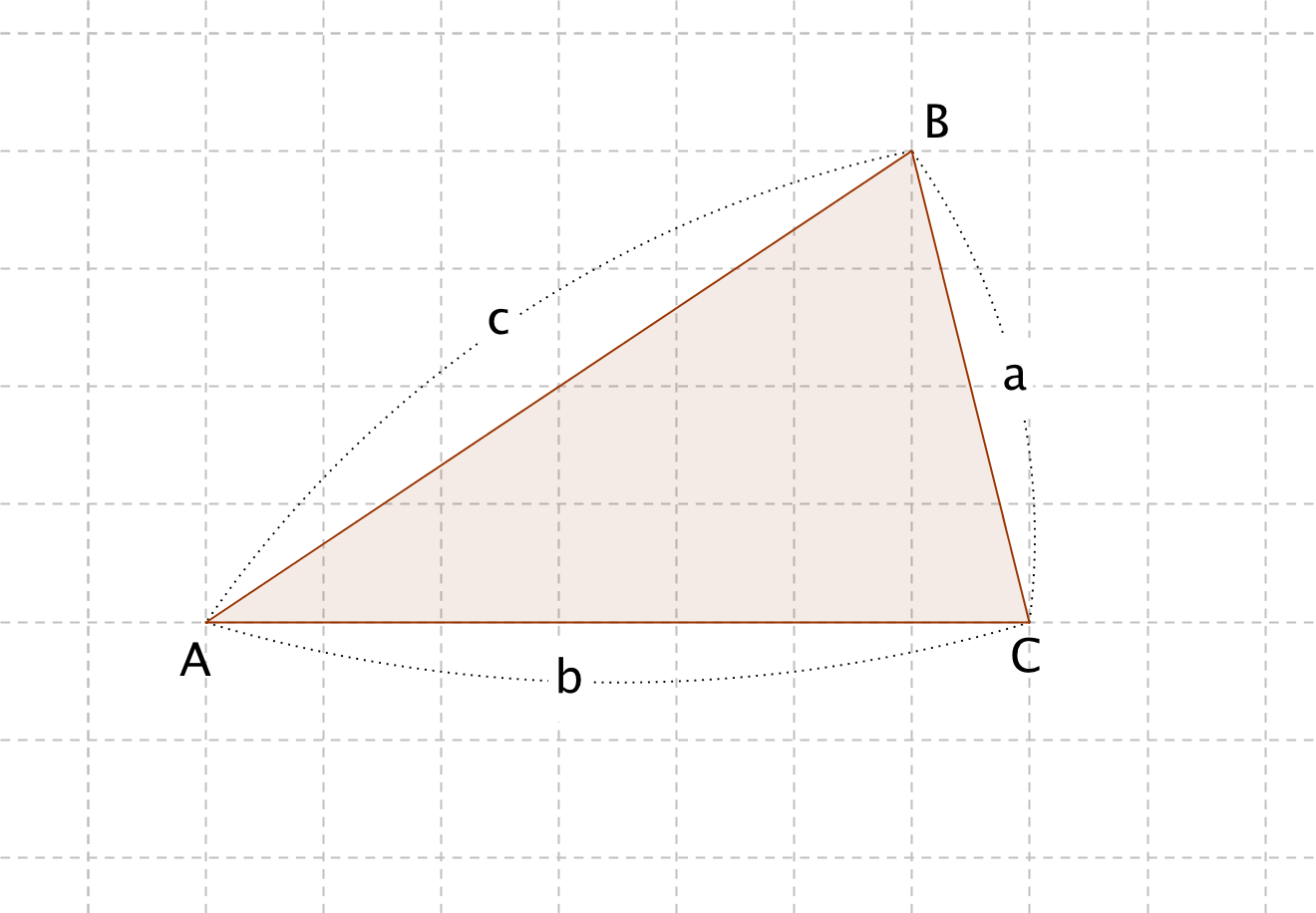



C言語入門 入力した3辺の長さから三角形の種類を判別 Webkaru



3



11 7 数学 図形 これは 不等辺三角形 ふとうへんさんかっけい ですか 辺が揃ってない三角形の話 のっぽさんの勉強メモ




二等辺三角形の定義と定理 算数 数学が好きになりmath
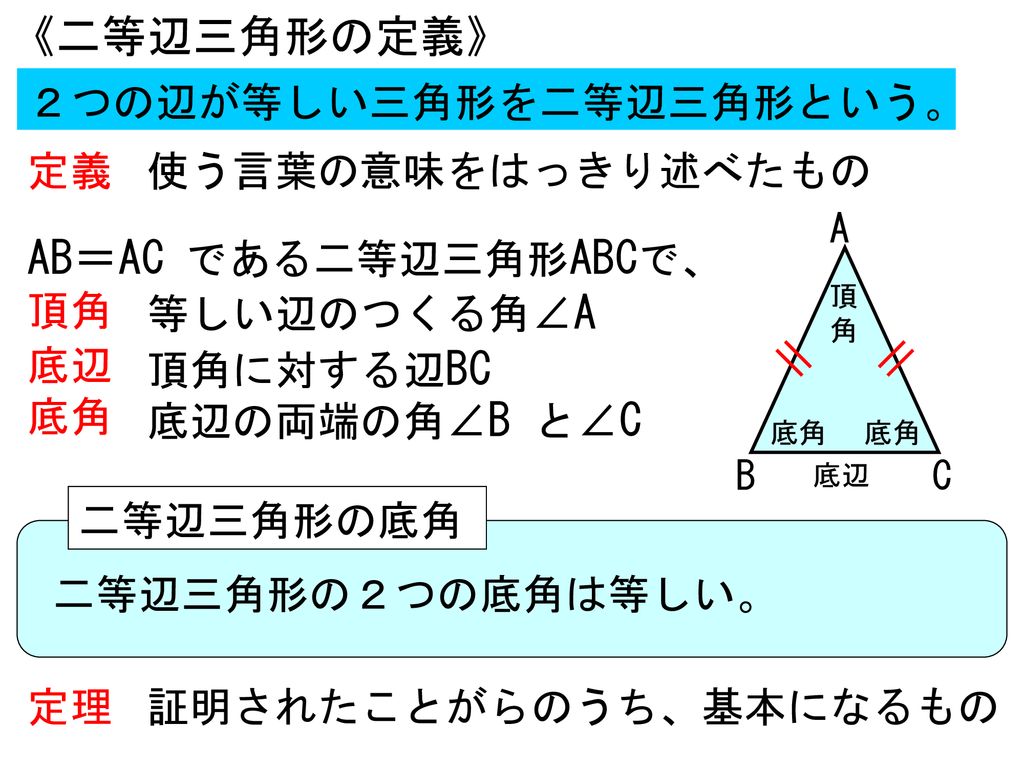



5 図形と合同 1章 三角形 1 二等辺三角形 4時間 Ppt Download
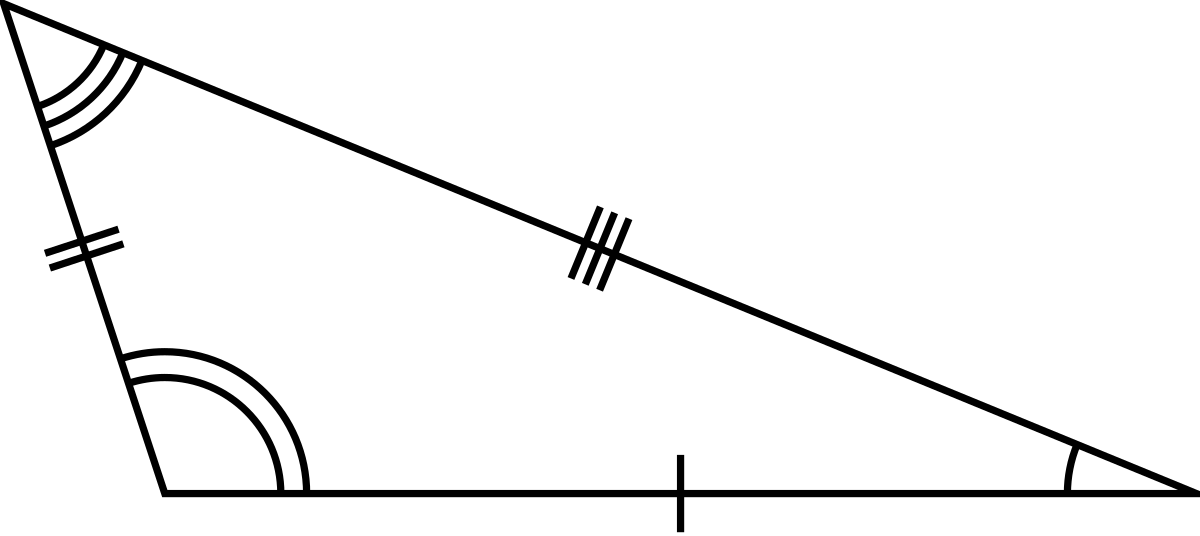



不等辺三角形 ウィクショナリー日本語版
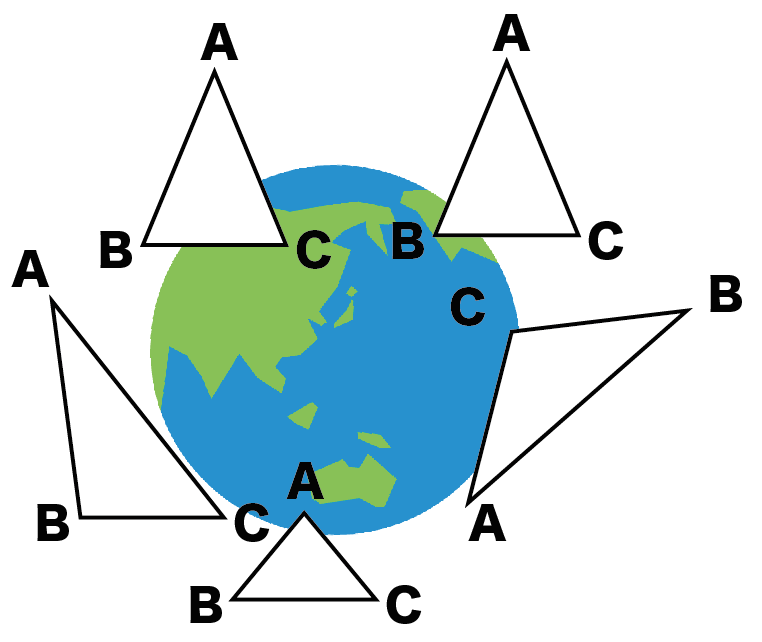



3分でわかる 二等辺三角形の定義 Qikeru 学びを楽しくわかりやすく



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




数学 中2 64 二等辺三角形 Youtube
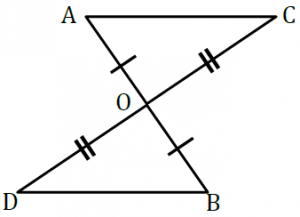



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン



このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋



Core Ac Uk Download Pdf Pdf




数学 色々な三角形の英単語まとめ 二等辺三角形 直角三角形ほか 英単語project




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学



0 件のコメント:
コメントを投稿